Goedel-Prover-V2 – An Open-Source Theorem Proving Model Jointly Developed by Princeton, Tsinghua, and Others

What is Goedel-Prover-V2?

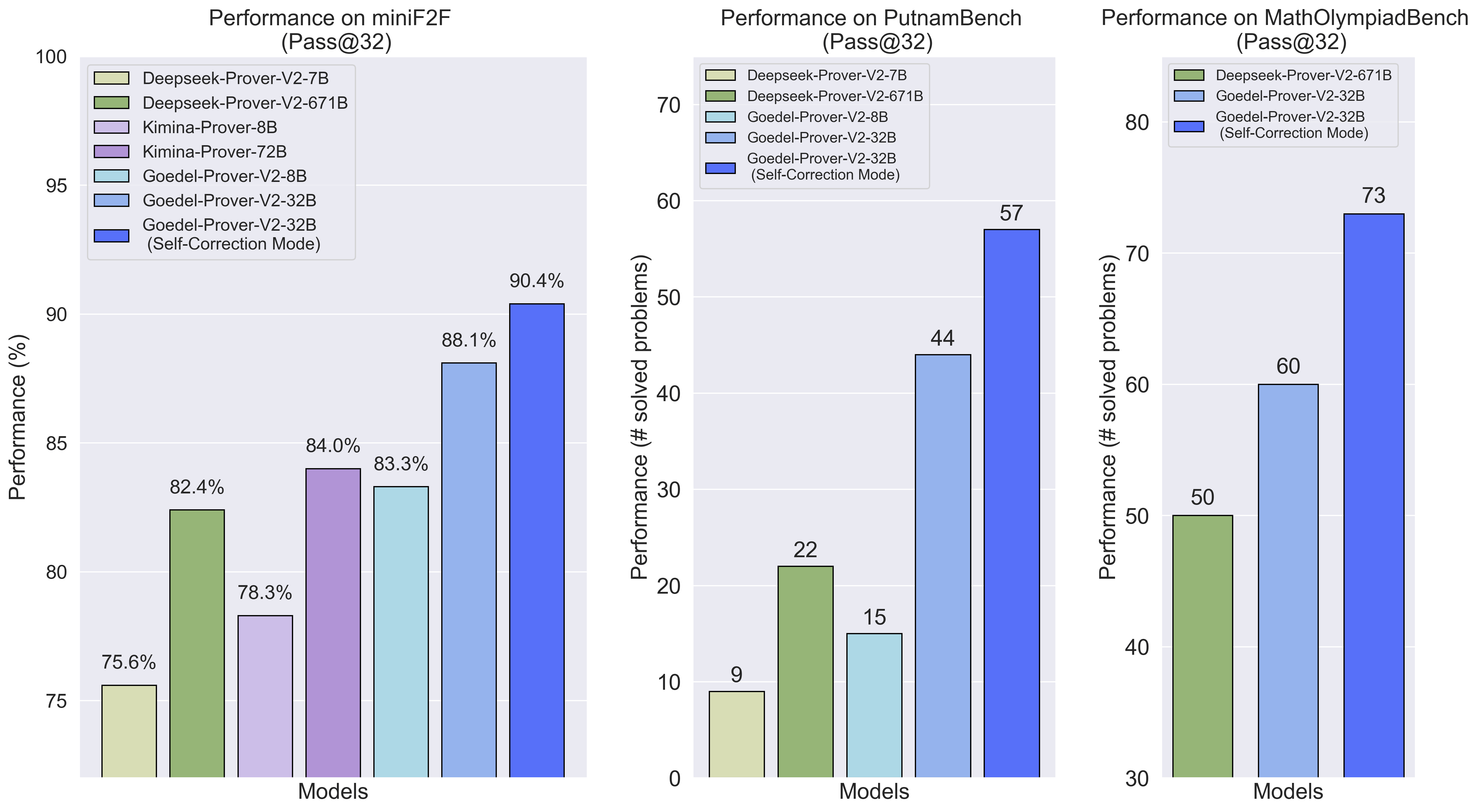
Goedel-Prover-V2 is an open-source theorem proving model jointly developed by leading institutions including Princeton University, Tsinghua University, and NVIDIA. Leveraging innovations such as scaffolded data synthesis, verifier-guided self-correction, and model averaging, Goedel-Prover-V2 significantly enhances performance in automated formal proof generation. The model is available in two parameter sizes: 32B and 8B. On the MiniF2F benchmark, the 32B model achieves a Pass@32 score of 90.4%, surpassing the previous state-of-the-art DeepSeek-Prover-V2 with 671B parameters. Goedel-Prover-V2 also ranks first on the PutnamBench and MathOlympiadBench benchmarks, demonstrating exceptional theorem-proving capabilities. This release marks a new milestone in the application of AI to formal mathematics.

Key Features of Goedel-Prover-V2

• Automated Proof Generation: Automatically generates formal proofs for complex mathematical problems.

• Self-Correction: Uses feedback from the Lean compiler to iteratively refine and improve its proofs.

• Efficient Training and Optimization: Employs scaffolded data synthesis and model averaging to enhance training effectiveness and model performance.

• Open-Source and Extensible: Provides open-source models and datasets, enabling researchers to further explore, extend, and improve the system.

Technical Innovations Behind Goedel-Prover-V2

• Scaffolded Data Synthesis: Generates proof tasks with progressively increasing difficulty, helping the model transition from simple to complex problems. Intermediate problems fill the gap between easy and hard tasks, providing denser training signals.

• Verifier-Guided Self-Correction: The model uses feedback from the Lean compiler to iteratively correct its proofs, closely mimicking how humans revise and refine mathematical arguments—resulting in improved accuracy and reliability.

• Model Averaging: Combines checkpoints from different training stages to recover model diversity. This significantly boosts performance under higher Pass@K values and enhances robustness.

Performance Highlights of Goedel-Prover-V2

MiniF2F Benchmark

• 32B Model:

  • Pass@32: Achieves 90.4%, significantly outperforming DeepSeek-Prover-V2-671B’s 82.4%.

  • Self-Correction Mode: Performance remains at 90.4% with iterative correction.

• 8B Model:

  • Pass@32: Reaches 83.3%, nearly matching DeepSeek-Prover-V2-671B, despite being almost 100× smaller in size.

PutnamBench Benchmark

• 32B Model:

  • Pass@64: Solves 64 problems, topping the leaderboard.

  • Pass@32: Solves 57 problems, far exceeding DeepSeek-Prover-V2-671B’s 47 problems.

• 8B Model:

  • Pass@32: Performs strongly, comparable to the 671B model.

MathOlympiadBench Benchmark

• 32B Model: Solves 73 problems, significantly ahead of DeepSeek-Prover-V2-671B’s 50 problems.

• 8B Model: Also performs competitively, showing powerful theorem-proving ability at a smaller scale.

Project Links for Goedel-Prover-V2

• Official Website: https://blog.goedel-prover.com/

• Hugging Face Model Repositories:

  • Goedel-Prover-V2-8B

  • Goedel-Prover-V2-32B

Application Scenarios of Goedel-Prover-V2

• Mathematical Theorem Proving: Automatically generates formal proofs for mathematical conjectures and theories, accelerating research and discovery in pure mathematics.

• Software and Hardware Verification: Validates the correctness of algorithms, program logic, and circuit designs using formal proofs—minimizing errors and improving the security and reliability of systems.

• Education: Acts as a teaching assistant, providing students with formal proof examples and helping them understand mathematical theorems and concepts.

• AI and Machine Learning: Verifies the theoretical foundations and algorithmic logic of AI/ML models to ensure accuracy and dependability.

• Scientific Research and Engineering: Helps validate mathematical models and theoretical assumptions in scientific and engineering contexts, ensuring the feasibility and soundness of designs and experiments.