DeepSeek-Math-V2 – DeepSeek’s open-source mathematical reasoning model

What is DeepSeek-Math-V2?

DeepSeek-Math-V2 is an open-source mathematical reasoning model released by the DeepSeek team, capable of performing self-verifying mathematical reasoning. The model focuses on answer correctness and emphasizes rigor in reasoning. By training both theorem-proof verifiers and generators and introducing a meta-verification mechanism, the model can review proof steps like a human mathematician and even correct itself. DeepSeek-Math-V2 performs exceptionally well on benchmarks such as IMO, CMO, and Putnam, achieving near-perfect scores. It is built upon DeepSeek-V3.2-Exp-Base and uses a co-evolution strategy between verifiers and generators to advance deep mathematical reasoning capabilities.

DeepSeek-Math-V2

Key Features of DeepSeek-Math-V2

1. Theorem Proving

The model can generate rigorous mathematical proofs for complex problems, including those from the International Mathematical Olympiad (IMO) and the Putnam Mathematics Competition.

2. Self-Verification

The model evaluates its own proofs, assessing correctness and rigor in a manner similar to a human mathematician’s self-review.

3. Error Detection & Correction

Through an honesty-based reward mechanism, the model evaluates its generated solutions, identifies its own mistakes, and corrects them—significantly reducing hallucinations.

4. Automated Training

By co-evolving the verifier and generator, the system automatically filters and labels difficult problems, continuously improving model performance.

Technical Principles of DeepSeek-Math-V2

1. Proof Verifier

A language-model-based verifier is trained to evaluate the correctness and rigor of mathematical proofs. It classifies proofs into three levels:

• Perfect (1 point)

• Small flaws (0.5 points)

• Fundamental errors (0 points)

The verifier also gives detailed commentary.

2. Meta-Verification

A “supervisor” role is introduced to re-check the verifier’s judgment, preventing incorrect scoring or hallucinated evaluations. This dual-layer verification ensures higher accuracy and reliability when assessing proofs.

3. Proof Generator

A generator trained for mathematical proof creation. After producing a proof, it performs self-evaluation. With the honesty reward mechanism, the model is encouraged to truthfully identify its own mistakes in exchange for reward signals.

4. Synergistic Co-evolution

Using a Student–Teacher–Supervisor collaborative framework, the generator and verifier improve together.

• The generator produces proofs

• The verifier evaluates them

• The system automatically identifies difficult or ambiguous problems
  These are fed back into training to continuously enhance the model.

5. Expanded Verification Compute

As the generator becomes stronger, the system expands verification capacity to automatically annotate hard-to-verify proofs, creating more training data and maintaining a dynamic balance between generation and verification.

Project Resources for DeepSeek-Math-V2

• GitHub Repository: https://github.com/deepseek-ai/DeepSeek-Math-V2

• HuggingFace Model: https://huggingface.co/deepseek-ai/DeepSeek-Math-V2

• Technical Paper: https://github.com/deepseek-ai/DeepSeek-Math-V2/blob/main/DeepSeekMath_V2.pdf

Performance of DeepSeek-Math-V2

IMO 2025 (International Mathematical Olympiad 2025)

DeepSeek-Math-V2 reaches gold-medal performance, demonstrating strong capability in solving highly challenging proof problems.

CMO 2024 (China Mathematical Olympiad 2024)

Also achieves gold-medal level performance, showing competitiveness in both international and national elite contests.

Putnam 2024

With extended verification compute, DeepSeek-Math-V2 nearly achieves a perfect score (118/120), approaching the level of top human contestants.

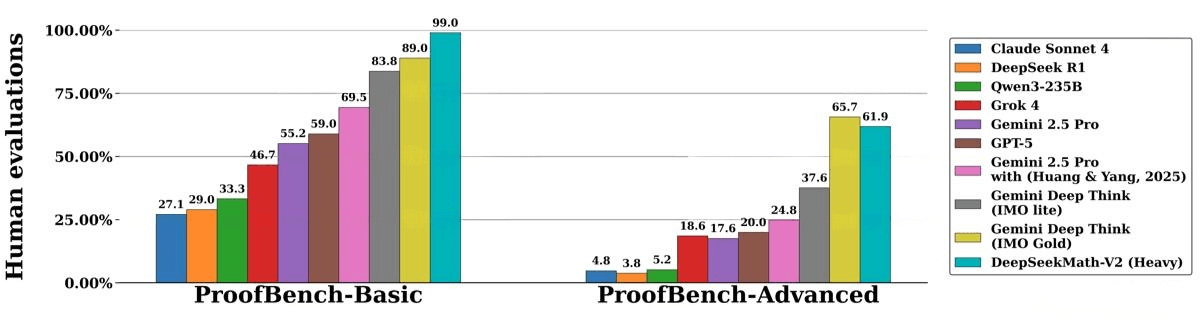
IMO-ProofBench Benchmark

• Basic subset: Nearly 99%, far surpassing other models

• Advanced subset: Slightly below Gemini Deep Think (IMO Gold) but still delivers strong performance, proving its ability on complex proofs

Application Scenarios of DeepSeek-Math-V2

1. Intelligent Tutoring Tools

Helps students understand and generate mathematical proofs, providing detailed solution steps and logical reasoning to support learning.

2. Theorem-Proving Assistance

Assists mathematicians in validating complex proofs, identifying logical gaps, and accelerating mathematical research.

3. Theoretical Physics

Supports physicists in deriving complex mathematical formulas and verifying the mathematical foundations of physical theories.

4. Reasoning Research

Serves as a benchmark model for studying mathematical reasoning and logical verification, advancing AI research in deep reasoning.

5. Math Competition Training

Provides high-quality practice problems and solution strategies, simulates competition environments, and helps contestants improve performance.